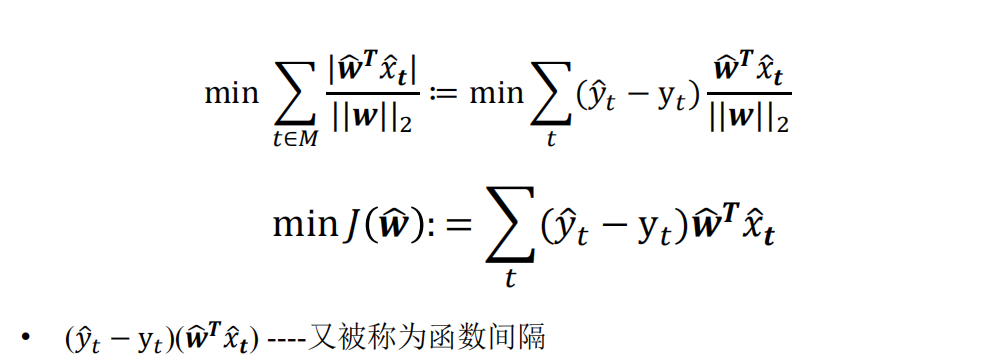ML-notes:人工神经网络
5 人工神经网络
本章讨论现阶段比较热门的一个监督学习算法————人工神经网络(artificial Neural Network)
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所做的交互反应。
5.1 神经元模型 Neuron
神经网络中最基本的成分便是神经元(Neuron)模型,也就是上面说的适应性简单单元。在神经网络中,每个神经元都与其他神经元相连,当它“兴奋”时,都会向相连的神经元发送化学物质,改变相连的神经元内的电位;如果神经元电位超过了一个“阈值”(threshold),那么该神经元就会兴奋,所以整个神经网络就是通过兴奋和电位来传播信息。
5.1.1 M-P神经元模型
1943年一直沿用至今的 “M-P神经元模型” 便是对这个过程的抽象。
在这个模型中,
- 神经元收到了来自其他 n 个神经元传递过来的输入信号 xi
- 而这些输入信号通过带有权重的连接(connection),这些权重又叫连接权(connection weight)。
- 然后来到细胞体的前部分,它负责计算总输入值(输入信号的加权求和,累积电平)
- 然后到达后部分,计算总输入值与神经元阈值的差值,通过激活函数(activation function)处理,传递到下一层神经元。
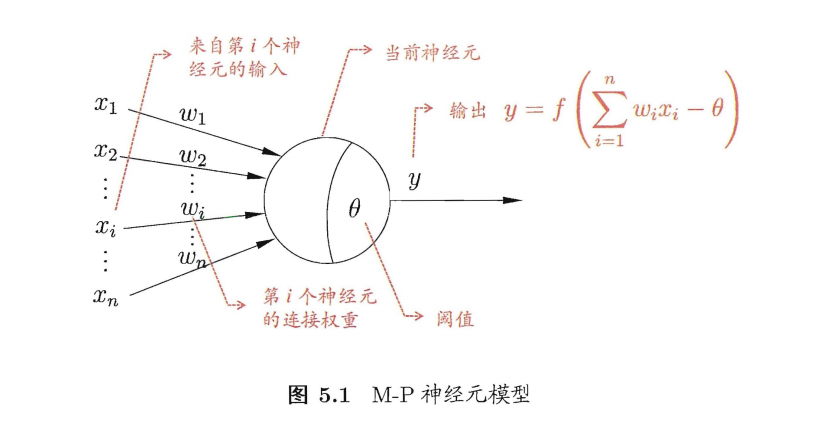
- ① 𝒙𝒊 来自第𝑖个神经元的输入
- ② 𝒘𝒊 第𝑖 个神经元的连接权重
- ③ 𝜽 阈值(threshold)或称为偏置 (bias)
- ④ y是输出,也是激活函数
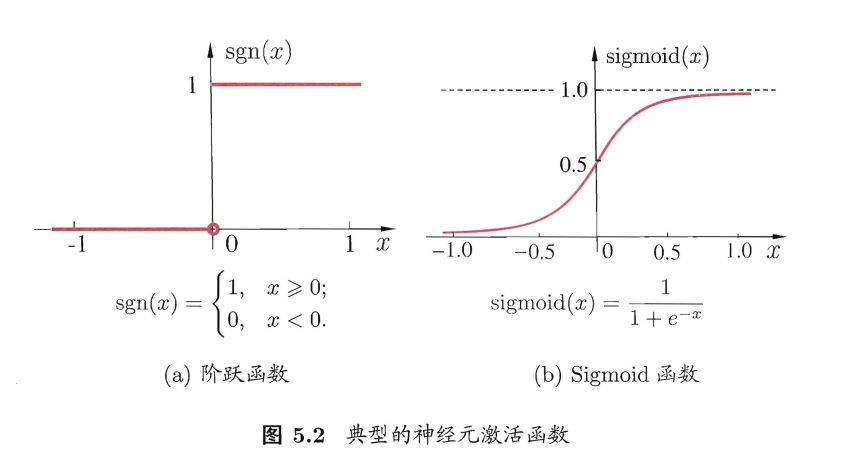
和之前讲的线性模型的分类十分相似,神经元模型最理想的激活函数也是阶跃函数。即将神经元输入值与阈值的差值映射为输出值 1 或 0 ,0 表示抑制神经元而 1 表示激活神经元。但阶跃函数不连续,不光滑,故在M-P神经元模型中,也采用Sigmoid函数来近似, Sigmoid函数将较大范围内变化的输入值挤压到 (0,1) 输出值范围内,所以也称为挤压函数(squashing function):
将多个神经元按一定的层次结构连接起来,就得到了神经网络。它是一种包含多个参数(输入)的模型,比方说10个神经元两两连接,则有100个参数需要学习(每个神经元有9个连接权以及1个阈值),若将每个神经元都看作一个函数,则整个神经网络就是由这些函数相互嵌套而成。
神经元模型与逻辑回归模型求解的优化问题是一致的,都是线性二分类问题。本质上来说,M-P神经元模型就等同于一个线性二分类器。
- Sigmoid函数≠Logistic函数
- Logistic函数⊂ Sigmoid函数
5.2 感知机(perceptron)与多层网络
5.2.1 感知机
概念
感知机(Perceptron) 是由两层神经元组成的一个简单模型。
只有输出层是M-P神经元,即只有输出层神经元进行激活函数处理,也称为阈值神经单元(threshold logic unit);也叫功能神经元。
输入层只是接受外界信号(样本属性)并传递给输出层(输入层的神经元个数等于样本的属性数目),而没有激活函数。
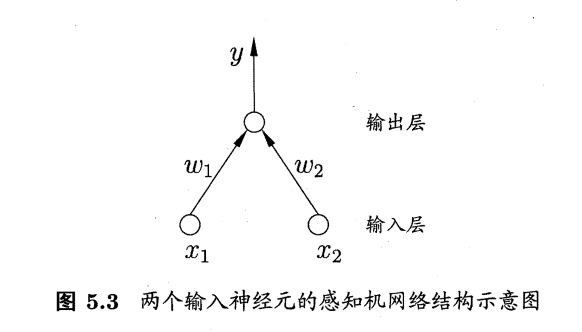
于是,感知机与之前线性模型中的对数几率回归的思想基本是一样的,都是通过对属性加权与另一个常数求和,再使用sigmoid函数将这个输出值压缩到0-1之间,从而解决分类问题。
不同的是感知机的输出层应该可以有多个神经元,从而可以实现多分类问题,同时两个模型所用的参数估计方法十分不同。
学习
给定数据集,权重 Wi(i = 1,2…,n)以及阈值 θ 可以通过学习得到。阈值 θ 可以看作一个固定的输入为 -1.0 的“哑结点”(dummy node)所对应的连接权重 wn+1,这样我们就可以i将权重与阈值的学习统一为权重学习。
感知机的学习规则非常简单,对于训练样例 (x,y),若当前感知机的输出为 y~,则感知机权重这样调整:
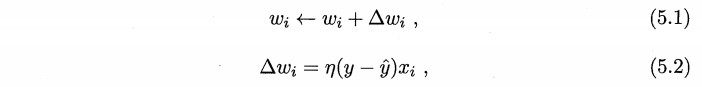
其中 ŋ ∈(0,1)称为学习率(learning rate)。从上图知道,如果预测正确,即样例的 y 与预测值 y~相等,则不会调整权重。
缺陷
感知机只有输出层神经元进行激活函数处理,也就是只有这一层功能神经元,学习能力有限。而 与、或、非问题都是线性可分(linearly separable)问题。对于这种线性可分问题,感知机的学习过程一定是收敛从而求得适当的权向量 w = (w1;w2;…;wn+1);不收敛的话,感知机就会发生振荡(fluctuation)。权向量难以稳定,无法求得合适解。
比如下面的非线性可分问题“异或”就无法解决:
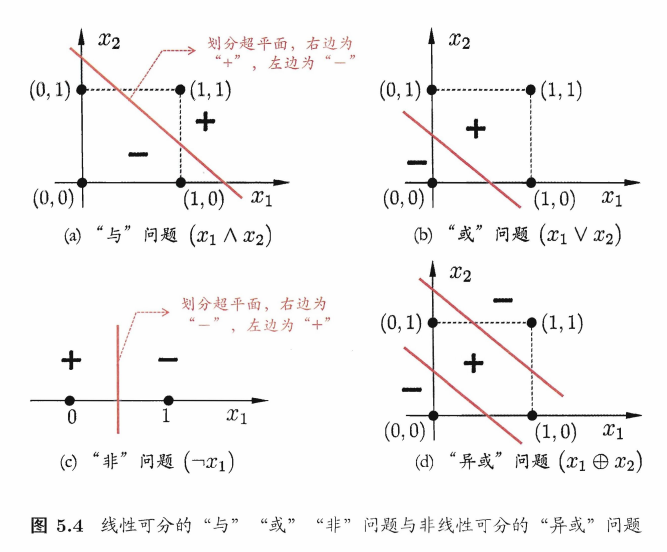
其实就是一个分类问题,当分类边界呈现非线性时感知机就无法解决了
点到超平面距离
上面有讲到点到超平面,这里讨论一下点到超平面的距离。
超平面(Hyperplane):超平面是n维欧氏空间中余维度等于一的线性子空间,也就是必须是(n-1)维度。其实相当于是一个n维空间的一种n-1维分界平面。
我们将数据向量化:
- 阈值 θ = w0:
- 所以可以将输出向量化如下图:
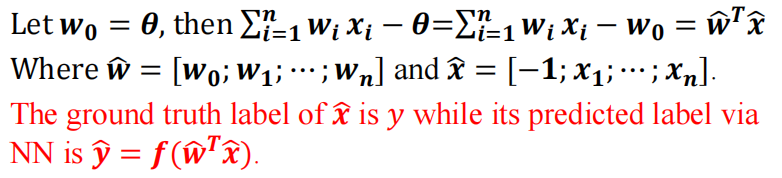
然后我们可以知道点到超平面(Hyperplane)的距离:

也就是 输出的值 det(wTx) 除以权值的2-范数 ||w||2
损失函数
损失函数的一个自然选择是误分类点的总数。但是这样的损失函数不是参数w和b的连续可导函数,不易优化。
所以我们将目标选到了最小化误分类点到分类平面的距离。得到以下结果:

而感知机的目标是使误分类点的个数为0,所以提出了新的概念叫函数间隔,以此简化学习过程: