3 线性模型

由于时间原因，这里只讲解部分内容

3.3 对数几率回归

虽然只讲这个，但是我们还是要提一提一些概念。

3.3.1 前情提要

  • 线性模型：其实我们很早就已经与它打过交道，比如我们熟知的“最小二乘法”。这就是线性模型的经典算法之一：根据给定的（x，y）点对，求出一条与这些点拟合效果最好的直线y=ax+b。
  • 线性回归：就是试图学到一个线性模型尽可能准确地预测新样本的输出值。
  • 监督学习：1.绪论的方法分类有提到。
  • 回归与分类：我们可以通过线性回归的思想来解决一些分类任务，比如二分类问题。

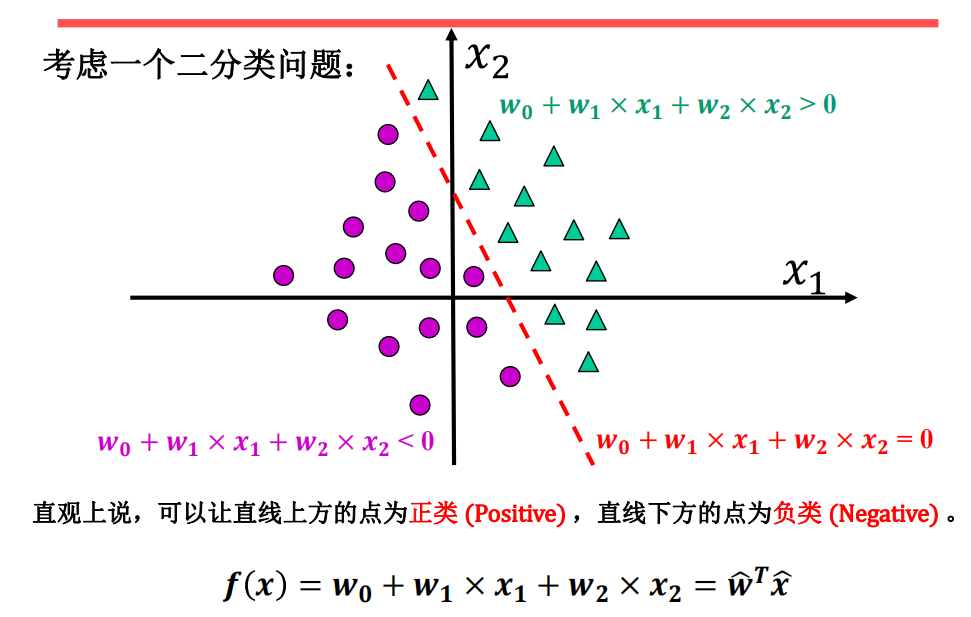
直观上说，可以规定直线上方的点为正样本(Positive) ，直线下方的点为负样本(Negative) 。本质上说，我们是需要把连续实数值转化为离散值的(例如: 𝟎, 𝟏)：

  • 比如：对于二分类任务，线性模型预测出来的是 连续值 z = wx + b，所以我们需要将 z 转换为 0/1 值，最理想的就是单位阶跃函数：

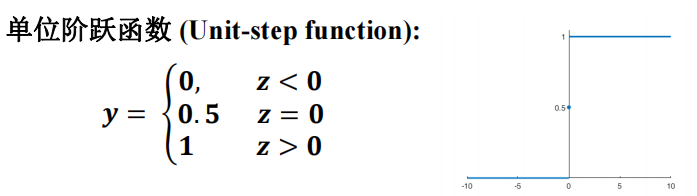
直观就是我们可以使用一个线性分类器𝒇(𝒙)，当𝒙为正类样本，𝒇 (𝒙) > 𝟎，反之， 𝒙 为负类样本，则 𝒇 (𝒙) < 𝟎 。

当然这只是一种基本分类思想，我们还需要对分类器的好坏进行度量，也就是上一章的模型评估与选择。当前的分类器是无法与标签相对应，自然也无法纠正分类错误，毕竟分类器的输出是线性的，而 标签 是离散的。（分类器 输出范围 [-∞，+∞]，而 标签 可以是{1，0}，{1，-1}）

然而单位阶跃函数是不好满足这个条件的，所以就提到了 对数几率函数。

3.3.2 对数几率函数

回归就是通过输入的属性值得到一个预测值，利用广义线性模型的特征，是否可以通过一个联系函数，将预测值转化为离散值从而进行分类呢？线性几率回归正是研究这样的问题。对数几率引入了一个对数几率函数（logistic function）,将预测值投影到 0-1 之间，从而将线性回归问题转化为二分类问题。单位阶跃函数不是一个连续函数，我们引入对数几率函数（logistic function）正好可以替代它：

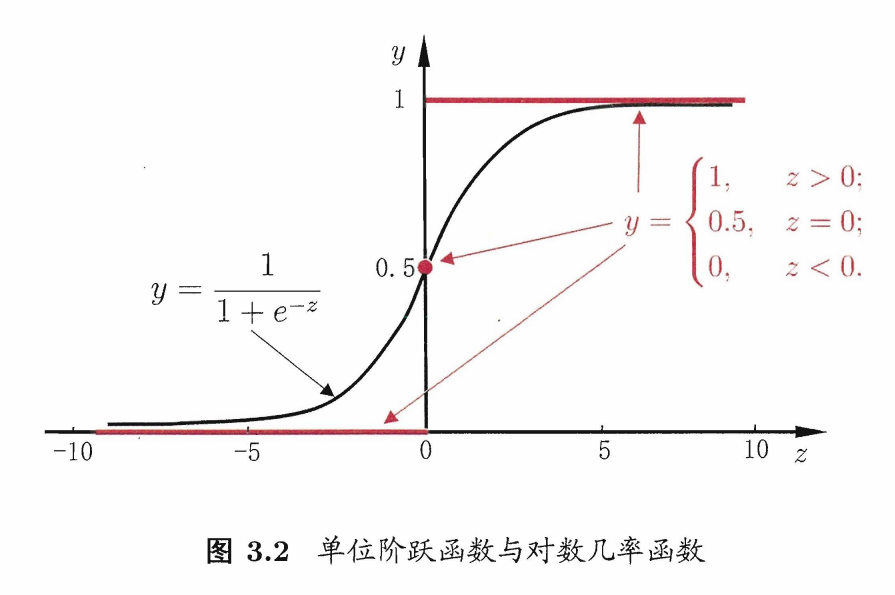
从图3.2可以看出，Logistic Function 对数几率函数是一种“Sigmoid”函数，它将 z 值转化为一个接近0 或 1 的值 y，并且输出值在 z = 0 附近变化很陡。

若将 y 视为样本作为正例的可能性，那么 1 - y 就是反例的可能性，则实际上这就是使用线性回归模型的预测结果器逼近真实标记的对数几率。因此这个模型称为 “对数几率回归”（logistic regression），也有一些书籍称之为“逻辑回归”。

两者的比值，我们称之为 几率 （odds），反应了 x 作为正例的相对可能性，而取对数就得到了 对数几率（log odds 又称 logit）。

几率 （odds）
对数几率（log odds 又称 logit）

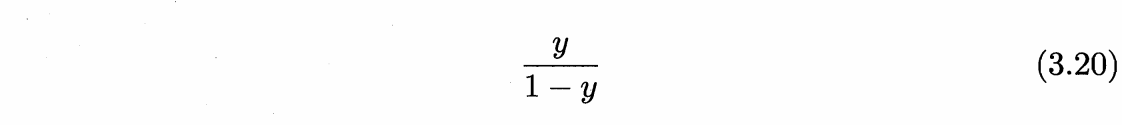
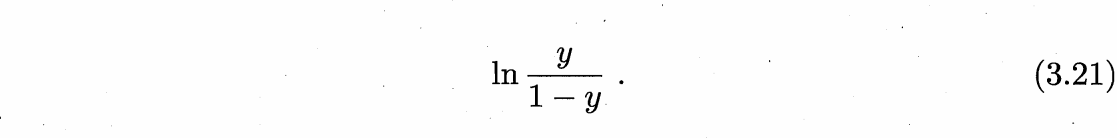
3.3.3 最大似然估计

我们可以使用最大似然估计的方法，求得下述对数几率模型的解 w,b。

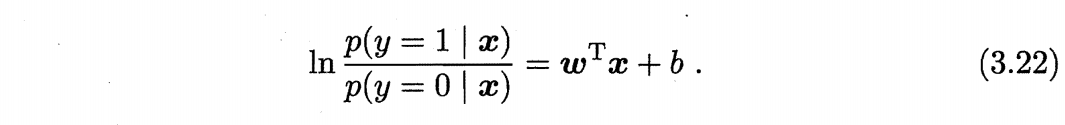
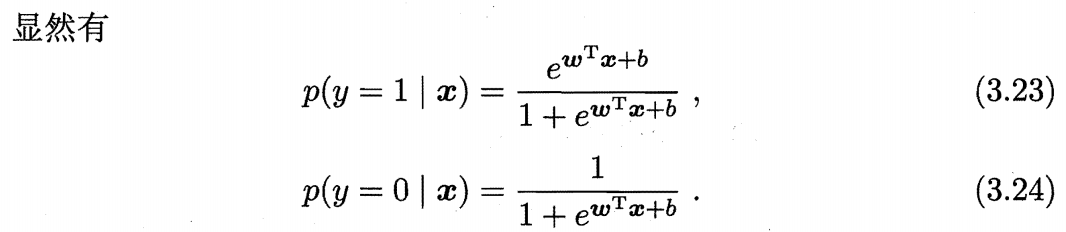
我们利用极大似然的思想构建目标函数： （3.23 正例概率 3.24 反例概率）
通过极大似然法，针对给定数据集{x,y}求解：

对数变乘为加，且采用了最大化似然（即所有样本出现真实值的概率乘积最大）

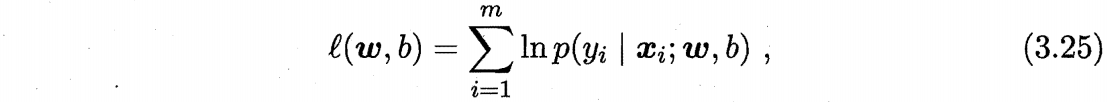
3.3.4 对数几率模型

所以：

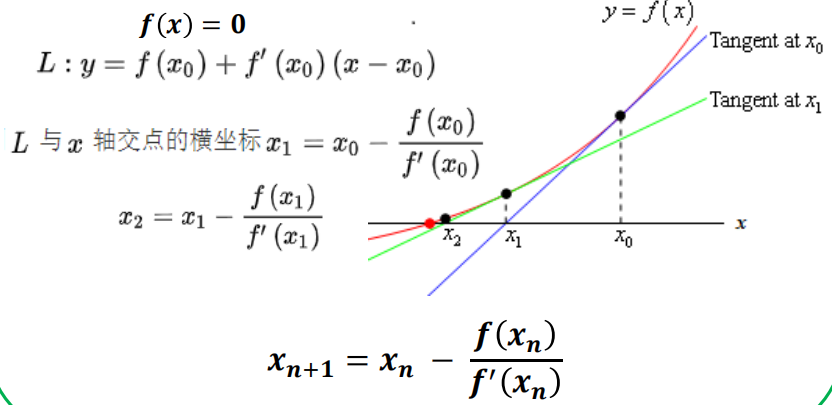
3.3.4.1 牛顿法（Newton’s Method）

牛顿法有两种应用方向，1、目标函数最优化求解， 2、方程的求解（根）

核心思想是对函数进行泰勒展开。

  • 方程求解：
用牛顿法可以解非线性方程，它是把非线性方程 f(x)=0 线性化的一种近似方法。把f(x)在点x0的某邻域内展开成泰勒级数。
取其线性部分（即泰勒展开的前两项），并令其等于0，即
以此作为非线性方程f(x)=0 的近似方程，若f’(xo)不为0，则其解为
这样，得到牛顿迭代法的一个迭代关系式：

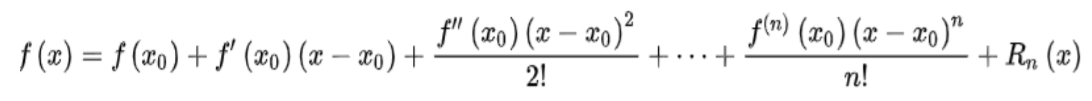
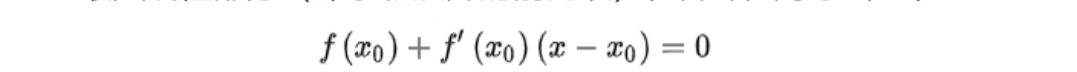
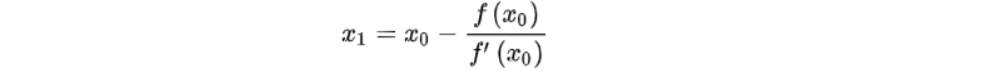
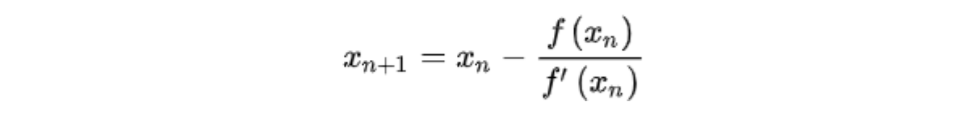
3.3.4.2 梯度下降法

梯度下降（gradient descent）在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

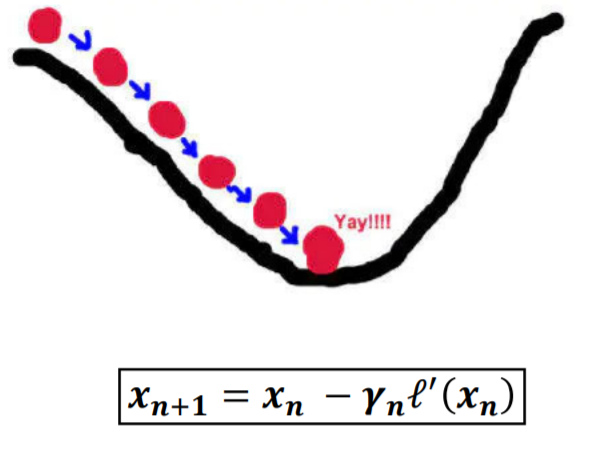
我们有个可微分的函数，它代表一座山。我们的目标是找到山底。梯度的方向是函数变化最快的方向也就是平地上最陡的方向。所以梯度下降的步骤是这样的：

  • 从一个出发点出发，我们开始求出发点的梯度
  • 向梯度方向的负方向行走一个步长
  • 重复求取梯度，重复行走步长
  • 直到走到底

3.3.5 总结

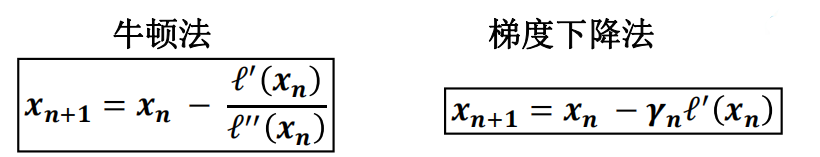
  • 牛顿法和梯度下降法是求解最优化问题的常见的两种算法。
  • 前者使用割线逐渐逼近最优解，后者使得目标函数逐渐下降。
  • 牛顿法的收敛速度快，但是需要二阶导数信息。
  • 梯度下降法计算速度快，但是需要人工确认步长参数。
  • 极大似然法：